In brief:
The Free Run experiment was first done to find the Q of the pendulum.
Later on it was repeated to see if kicking the ellipse to the other rotational direction would restore.
It did not.
Experiment to determine the Q of the pendulum.
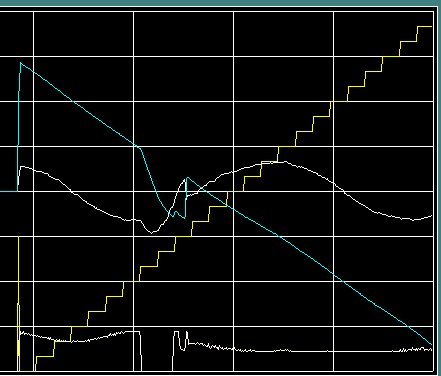
Fig. 1.
Light blue: Precession angle. Scale: +180 .. -180 deg.
Yellow staircase: time of the day in hour steps.
White centered: Minor axis of ellipse. Scale: 45 mm/div
White bottom averaged drive pulse width.
While the pendulum was running nicely with an angle of ca 45 deg I stopped the drive pulses at 07:00.
We see the amplitude of the minor axis first grow further CCW and than, more rapidly, go to CCW.
At 08:52 the drive pulses were enabled again and the pendulum resumed its normal run. It looks like the Foucault plane continued where it should be, but that is par hazard, I just restarted the pendulum for another experiment.
Data source: 2024-08-13.log

Fig. 2.
Animation of 939 screenshots form the compass display, at intervals of 10 seconds.
The movie starts at NE, when the drive pulses were switched off.
Just over ESE the pulses were switched on again, and we see the amplitude grow to 230 mm.
To obtain the decay curve I've measured the amplitudes of the major axis manually on the screen of these compass images at intervals of 1 minute.
This gave me the following graph:
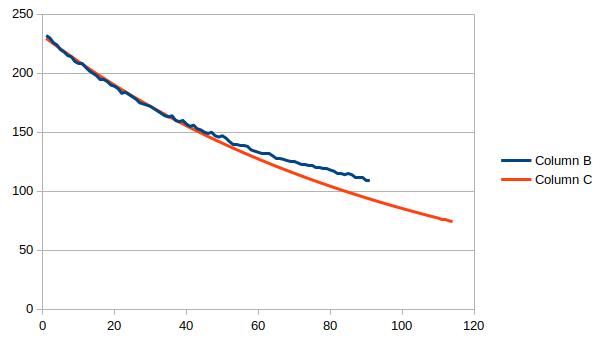
Fig 3.
Horizontal timescale is minutes from stopping the drive pulses.
Decay curve of pendulum amplitude (blue) and calculated e-x function for comparison (red).
We see that the pendulum decay deviates from the pure e-power function. This can be explained by the non linear air friction characteristic. At low speeds the frictional loss is relatively smaller than at the higher speeds, which results in a higher Q.
However, as we are interrested in the Q mainly because of the "Schumacher equation" we should use the data from the higher speed region.
To calculate the Q I took the time the red curve needs to reach half its value. That is after 70 minutes. In that time my pendulum does 70 x 60 / 4.16 = 1010 full swings. Multiplied by 4.53 gives a Q of 4578. (This calculation was made in the spreadsheet)
On 2024-09-05 I did two experiments where the drive pulses were disabled and after some time the ellips was kicked to the other direction.
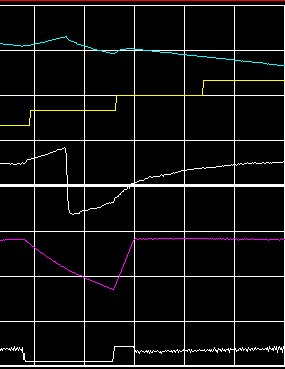
Fig. 4 Fig. 5
Legend fig. 4:
light blue: FP angle
Yellow staircase Time of the day, starting at 16:40
White: Minor axis (zero = centerline)
Purple: Major axis (zero = bottom)
White: averaged drive pulse width.
Timeline:
16:51 Start screenshots Dir = CCW
16:56 Disable Drive
17:25 Kick to CW
17:57 Enable Drive
19:00 End of test
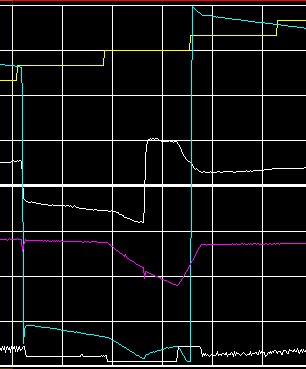
Fig. 6 Fig.7
Legend: as Fig 4. Time starts at 19:50
Timeline:
20:03 Relaunch -140 deg. ... let it stabilaize CW
21:02 Disable Drive
21:28 Kick to CCW
21:50 Enable Drive
23:00 End of test.
Conclusion: When the pendulum is not driven the rotational direction of the ellipse has no prefrence, when it is kicked to the other direction it just stays that way.
We can see that te precession of the ellips goes in the direction of the rotation. I'll stil check if the precession speed agrees with the formula (9) in the Theory chapter.